ZADANIA NA MARZEC 2024
Regulamin

1. Liga zadaniowa trwa od stycznia do maja w roku szkolnym 2023/24
2. Mogą do niej przystąpić wszyscy uczniowie z klas V-VIII ze Szkoły Podstawowej w Karsinie.
3. Do Ligi można przystąpić w dowolnym momencie i robić dowolnie długie przerwy.
4. Na początku każdego miesiąca na stronie internetowej zostaną opublikowane zadania. Pełne rozwiązania zadań (nie tylko odpowiedzi) należy dostarczać na podpisanej kartce nauczycielkom matematyki p. Aleksandrze Ossowskiej lub p. Elżbiecie Łosińskiej do końca danego miesiąca lub za pomocą e-dziennika (w postaci załącznika).
5. Punktacja będzie przedstawiana systematycznie po sprawdzeniu prac na początku każdego miesiąca na tablicy ogłoszeniowej.
6. Na zakończenie uczestnicy ligi napiszą test końcowy zawierający wybrane zadania z poszczególnych miesięcy oraz zadania „na szóstkę” z podręczników.
7. Na zakończenie roku szkolnego najlepsi uczniowie oraz autorzy wyjątkowo ciekawych rozwiązań w poszczególnych miesiącach otrzymają dyplomy, nagrody-niespodzianki oraz pochwały.

Zadania na marzec dla klas V – VI

Zad.1
Właściciel hurtowni w pierwszym tygodniu nowego miesiąca sprzedał 12% towaru, a drugim tygodniu 25% reszty. Oblicz, jaki procent towaru pozostał do sprzedaży po dwóch tygodniach działalności, jeśli nowych dostaw nie było.

Zad.2
Do wykonania bezy potrzebne są następujące składniki: 6 białek, 30 dag cukru, jedna łyżka soku z cytryny, szczypta soli. Alina ma tylko 4 białka i ma zamiar upiec z tego przepisu mniejszą porcję. Ile cukru musi użyć? Zapisz obliczenia.

Zad.3
Pewien kurs miał trwać 33h i odbywał się w formie trzynastu spotkań trwających 2 lub 3 godziny. Ile odbyło się spotkań krótszych, a ile dłuższych? Uzasadnij odpowiedź.

Zad.4
Prostokąt ma wymiary 12 cm x 8 cm. Jak można powiększyć jego wymiary, aby pole wzrosło o 25%? Podaj wszystkie możliwości.

Zadania na marzec dla klas VII – VIII

Zad.1.
Oblicz sumę wszystkich czynników pierwszych liczby 9350, jeżeli największy z nich wynosi 17.

Zad.2 
Wojtek przechowuje 24 standardowe sześcienne kostki do gry w zamkniętym pudełku o pojemności 0,6 litra. Każda z tych kostek ma krawędź o długości 1,5cm. Oblicz, ile procent pojemności pudełka wypełniają wszystkie te kostki. Zapisz obliczenia.

Zad.3
Siostry Basia i Kasia zbierają pieniądze na wycieczkę. Basia uzbierała 115% kwoty, którą zebrała Kasia. Gdy każda dziewczynka dostała od dziadków dodatkowo po 232zł, okazało się, że kwota uzbierana przez Kasię stanowi 92% kwoty zebranej przez Basię. Oblicz, ile pieniędzy uzbierała każda z dziewcząt. Zapisz obliczenia.

Zad.4 
Prostokąt ABCD o wymiarach 7 cm i 8 cm rozcięto wzdłuż prostej a na dwa trapezy tak, jak pokazano na rysunku. Odcinek CL ma długość 3,2cm.

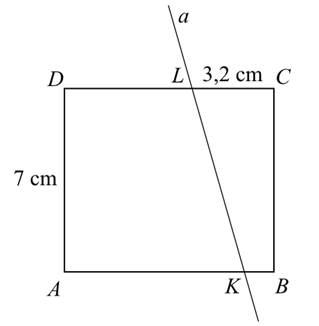
Pole trapezu KBCL jest czterokrotnie mniejsze od pola prostokąta ABCD. Oblicz długość odcinka KB. Zapisz obliczenia.

Zad.5
W wyborach na przewodniczącego klasy kandydowało troje uczniów: Jacek, Helena i Grzegorz. Każdy uczeń tej klasy oddał jeden ważny głos. Jacek otrzymał 9 głosów, co stanowiło 36% wszystkich głosów. Helena otrzymała o 6 głosów więcej niż Grzegorz. Oblicz, ile głosów otrzymała Helena, a ile – Grzegorz. Zapisz obliczenia.

Zad.6
Pan Karol rozważa kupno komputera. Przy płatności jednorazowej kosztuje on 2500zł. Przy zakupie na raty cena tego komputera jest o 8% wyższa – w momencie zakupu trzeba wpłacić 20% jego podwyższonej wartości, a pozostała kwota jest rozłożona na 12 równych części (rat). Oblicz wysokość każdej z tych rat.

opr. Elżbieta Łosinska, Aleksandra Ossowska